ஒரு முழுமையான சங்கிலி மற்றும் ஒரு சங்கிலியின் ஒரு பகுதிக்கான ஓம் விதி: சூத்திர விருப்பங்கள், விளக்கம் மற்றும் விளக்கம்

மூடிய சுற்றுக்கு

மூடிய சுற்று என்பது மின்னோட்டம் சுற்றும் ஒரு மூடிய மின் இணைப்பு என்று பொருள். ஒரு தொடர் கம்பிகள் ஒன்றோடொன்று இணைக்கப்பட்டு, சுற்று முடிவடையும் போது, ​​நான் வட்டத்தின் ஒரு முனையிலிருந்து மற்றொன்றுக்கு ஓடுகிறேன், அது ஒரு மூடிய சுற்று ஆகும்.

EMF (E) - வோல்ட்களில் குறிக்கப்படுகிறது மற்றும் அளவிடப்படுகிறது மற்றும் ஃபாரடே விதியின்படி பேட்டரி அல்லது காந்த சக்தியால் உருவாக்கப்பட்ட மின்னழுத்தத்தைக் குறிக்கிறது, இது நேரம் மாறுபடும் காந்தப்புலம் ஒரு மின்னோட்டத்தைத் தூண்டும் என்று கூறுகிறது.

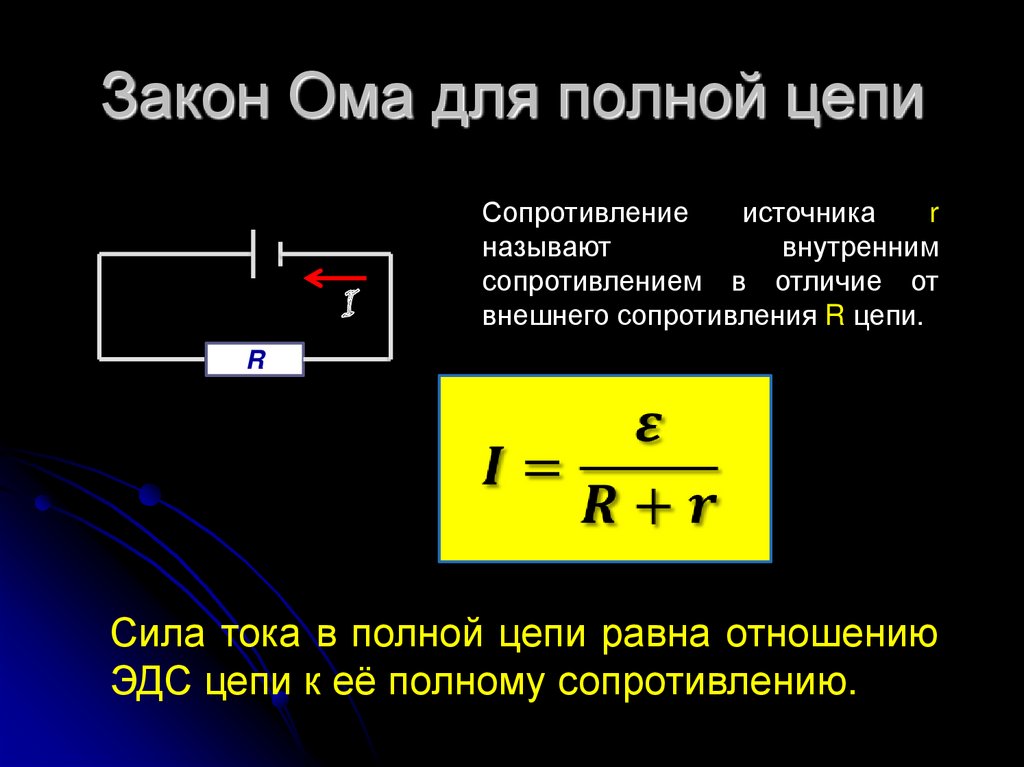
பின்னர்: E = IR + Ir

E \u003d I (R + r)

I \u003d E / (R + r)

எங்கே: r என்பது தற்போதைய மூலத்தின் எதிர்ப்பாகும்.

இந்த வெளிப்பாடு மூடிய வளைய சுற்றுகளின் ஓம் விதி என்று அழைக்கப்படுகிறது.

பன்முக சங்கிலி

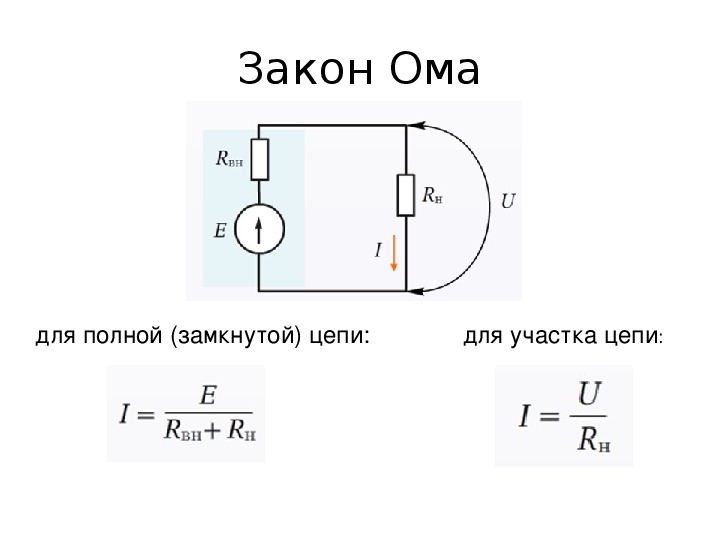
தனி பிரிவு மற்றும் முழுமையான மின்சுற்று

ஓம் விதி, ஒரு பிரிவு அல்லது முழு சுற்றுக்கு பயன்படுத்தப்படும், இரண்டு கணக்கீட்டு விருப்பங்களில் கருதலாம்:

• தனி குறுகிய பகுதி. இது EMF ஆதாரம் இல்லாத சுற்றுகளின் ஒரு பகுதியாகும்.
• ஒன்று அல்லது அதற்கு மேற்பட்ட பிரிவுகளைக் கொண்ட முழுமையான சங்கிலி. இது அதன் சொந்த உள் எதிர்ப்பைக் கொண்ட EMF மூலத்தையும் உள்ளடக்கியது.

மின்சுற்றின் தற்போதைய பிரிவின் கணக்கீடு

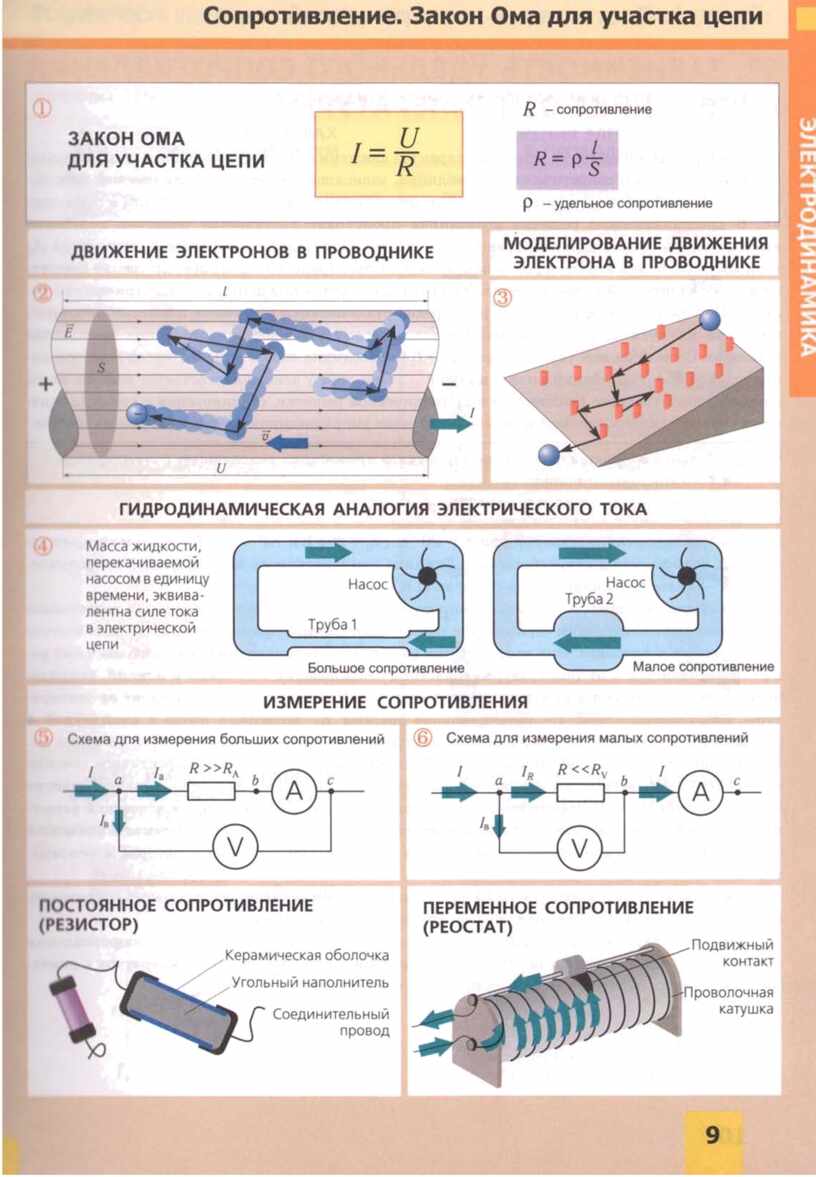
இந்த வழக்கில், அடிப்படை சூத்திரம் I \u003d U / R பயன்படுத்தப்படுகிறது, இதில் I தற்போதைய வலிமை, U என்பது மின்னழுத்தம், R என்பது எதிர்ப்பு. அதன் படி, ஓம் விதியின் பொதுவாக ஏற்றுக்கொள்ளப்பட்ட விளக்கத்தை ஒருவர் உருவாக்கலாம்:

கிராஃபிக் வடிவமைப்பில் "கெமோமில்" என்று அழைக்கப்படும் பல சூத்திரங்களுக்கு இந்த உருவாக்கம் அடிப்படையாகும். துறையில் P - சக்தி தீர்மானிக்கப்படுகிறது, துறைகளில் I, U மற்றும் R - தற்போதைய வலிமை, மின்னழுத்தம் மற்றும் எதிர்ப்பு தொடர்பான நடவடிக்கைகள் மேற்கொள்ளப்படுகின்றன.

ஒவ்வொரு வெளிப்பாடு - அடிப்படை மற்றும் கூடுதல், நீங்கள் சுற்று பயன்படுத்த நோக்கம் உறுப்புகளின் சரியான அளவுருக்கள் கணக்கிட அனுமதிக்கிறது.

மின்சுற்றுகளுடன் பணிபுரியும் வல்லுநர்கள் படத்தில் காட்டப்பட்டுள்ள முக்கோண முறையைப் பயன்படுத்தி எந்த அளவுருக்களையும் விரைவாக தீர்மானிப்பார்கள்.

கணக்கீடுகள் பிரிவின் உறுப்புகளை இணைக்கும் கடத்திகளின் எதிர்ப்பை கணக்கில் எடுத்துக்கொள்ள வேண்டும். அவை வெவ்வேறு பொருட்களிலிருந்து தயாரிக்கப்படுவதால், இந்த அளவுரு ஒவ்வொரு விஷயத்திலும் வித்தியாசமாக இருக்கும்.ஒரு முழுமையான சுற்று உருவாக்குவது அவசியமானால், முக்கிய சூத்திரம் மின்னழுத்த மூலத்தின் அளவுருக்களுடன் கூடுதலாக வழங்கப்படுகிறது, எடுத்துக்காட்டாக, ஒரு பேட்டரி.

ஒரு முழுமையான சங்கிலிக்கான கணக்கீட்டு விருப்பம்

ஒரு முழுமையான சுற்று என்பது ஒரு மின்னழுத்த மூலத்துடன் (EMF) தனித்தனி பிரிவுகளைக் கொண்டுள்ளது. இவ்வாறு, பிரிவுகளின் தற்போதைய எதிர்ப்பு இணைக்கப்பட்ட மூலத்தின் உள் எதிர்ப்பால் கூடுதலாக வழங்கப்படுகிறது. எனவே, முன்னர் விவாதிக்கப்பட்ட முக்கிய விளக்கம் பின்வருமாறு வாசிக்கப்படும்: I = U / (R + r). இங்கே, EMF மூலத்தின் எதிர்ப்பு காட்டி (r) ஏற்கனவே சேர்க்கப்பட்டுள்ளது.

தூய இயற்பியலின் பார்வையில், இந்த காட்டி மிகச் சிறிய மதிப்பாகக் கருதப்படுகிறது. இருப்பினும், நடைமுறையில், சிக்கலான சுற்றுகள் மற்றும் சுற்றுகளை கணக்கிடும் போது, ​​வல்லுநர்கள் அதை கணக்கில் எடுத்துக்கொள்ள வேண்டிய கட்டாயத்தில் உள்ளனர், ஏனெனில் கூடுதல் எதிர்ப்பு வேலையின் துல்லியத்தை பாதிக்கிறது. கூடுதலாக, ஒவ்வொரு மூலத்தின் அமைப்பும் மிகவும் பன்முகத்தன்மை வாய்ந்தது, இதன் விளைவாக, சில சந்தர்ப்பங்களில் எதிர்ப்பை மிக அதிக விகிதங்களில் வெளிப்படுத்தலாம்.

மேலே உள்ள கணக்கீடுகள் DC சுற்றுகள் தொடர்பாக செய்யப்படுகின்றன. மாற்று மின்னோட்டத்துடன் செயல்கள் மற்றும் கணக்கீடுகள் வேறுபட்ட திட்டத்தின் படி செய்யப்படுகின்றன.

ஒரு மாறி மீது சட்டத்தின் விளைவு

மாற்று மின்னோட்டத்துடன், மின்சுற்றின் எதிர்ப்பானது மின்மறுப்பு என்று அழைக்கப்படும், செயலில் எதிர்ப்பு மற்றும் எதிர்வினை எதிர்ப்பு சுமை ஆகியவற்றைக் கொண்டிருக்கும். தூண்டல் பண்புகள் மற்றும் ஒரு சைனூசாய்டல் தற்போதைய மதிப்பு கொண்ட உறுப்புகள் இருப்பதால் இது ஏற்படுகிறது. மின்னழுத்தமும் ஒரு மாறி, அதன் மாறுதல் விதிகளின்படி செயல்படுகிறது.

எனவே, ஓம் சட்டத்தின்படி ஒரு ஏசி சுற்று குறிப்பிட்ட விளைவுகளை கணக்கில் எடுத்துக்கொண்டு கணக்கிடப்படுகிறது: மின்னழுத்தத்திலிருந்து மின்னோட்டத்தின் அளவை வழிநடத்துதல் அல்லது பின்தங்குதல், அத்துடன் செயலில் மற்றும் எதிர்வினை சக்தியின் இருப்பு.இதையொட்டி, எதிர்வினை தூண்டல் அல்லது கொள்ளளவு கூறுகளை உள்ளடக்கியது.

இந்த நிகழ்வுகள் அனைத்தும் Z \u003d U / I அல்லது Z \u003d R + J * (XL - XC) சூத்திரத்துடன் ஒத்திருக்கும், இதில் Z என்பது மின்மறுப்பு; ஆர் - செயலில் சுமை; XL, XC - தூண்டல் மற்றும் கொள்ளளவு சுமைகள்; ஜே என்பது திருத்தக் காரணி.

ஒரு முழுமையான சர்க்யூட்டில் EMF ஆதாரம்

ஒரு மூடிய சுற்றில் மின்சாரம் ஏற்படுவதற்கு, இந்த சுற்று குறைந்தபட்சம் ஒரு சிறப்பு உறுப்பு கொண்டிருக்க வேண்டும், அதில் அதன் துருவங்களுக்கு இடையில் கட்டணங்களை மாற்றும் வேலை நடைபெறும். இந்த உறுப்புக்குள் கட்டணங்களை சுமக்கும் சக்திகள் மின்சார புலத்திற்கு எதிராக அவ்வாறு செய்கின்றன, அதாவது அவற்றின் இயல்பு மின்சாரத்திலிருந்து வேறுபட்டதாக இருக்க வேண்டும். எனவே, அத்தகைய சக்திகள் மூன்றாம் தரப்பு என்று அழைக்கப்படுகின்றன.

அரிசி. 1. இயற்பியலில் வெளிப்புற சக்திகள்.

மின்சுற்றின் ஒரு உறுப்பு, இதில் வெளிப்புற சக்திகள் மின்சார புலத்தின் செயல்பாட்டிற்கு எதிராக கட்டணங்களை மாற்றுவதற்கு வேலை செய்யும் ஒரு உறுப்பு தற்போதைய ஆதாரம் என்று அழைக்கப்படுகிறது. அதன் முக்கிய பண்பு வெளிப்புற சக்திகளின் அளவு. அதை வகைப்படுத்த, ஒரு சிறப்பு நடவடிக்கை அறிமுகப்படுத்தப்பட்டது - எலக்ட்ரோமோட்டிவ் ஃபோர்ஸ் (EMF), இது $\mathscr{E}$ என்ற எழுத்தால் குறிக்கப்படுகிறது.

தற்போதைய மூலத்தின் EMF இன் மதிப்பு இந்த கட்டணத்தின் மதிப்புக்கு கட்டணத்தை மாற்றுவதற்கான வெளிப்புற சக்திகளின் விகிதத்திற்கு சமம்:

$$\mathscr{E}={A_{st}\over q}$$

EMF இன் பொருள் மின் மின்னழுத்தத்தின் அர்த்தத்திற்கு மிக நெருக்கமாக இருப்பதால் (நினைவுபடுத்தவும், மின்னழுத்தம் என்பது மின்னழுத்தம் செய்யும் வேலையின் விகிதமாகும். மின்னழுத்தங்கள்:

$$1B={J\overCl}$$

உண்மையான மின்னோட்ட மூலத்தின் இரண்டாவது மிக முக்கியமான மின் பண்பு அதன் உள் எதிர்ப்பாகும்.டெர்மினல்களுக்கு இடையில் கட்டணங்கள் மாற்றப்படும்போது, ​​அவை EMF மூலத்தின் பொருளுடன் தொடர்பு கொள்கின்றன, எனவே, மின்னோட்டத்திற்கான மூலமும் சில எதிர்ப்பை அளிக்கிறது. உள் எதிர்ப்பானது, சாதாரண எதிர்ப்பைப் போலவே, ஓம்ஸில் அளவிடப்படுகிறது, ஆனால் சிறிய லத்தீன் எழுத்து $r$ மூலம் குறிக்கப்படுகிறது.

அரிசி. 2. தற்போதைய ஆதாரங்களின் எடுத்துக்காட்டுகள்.

ஆர் - மின் எதிர்ப்பு

எதிர்ப்பு என்பது மின்னழுத்தத்தின் பரஸ்பரம் மற்றும் ஓடும் நீரில் இயக்கத்திற்கு எதிராக உடலை நகர்த்துவதன் விளைவுடன் ஒப்பிடலாம். R இன் அலகு ஓம் ஆகும், இது பெரிய கிரேக்க எழுத்தான ஒமேகாவால் குறிக்கப்படுகிறது.

எதிர்ப்பின் எதிரொலி (1/R) கடத்துத்திறன் என அழைக்கப்படுகிறது, இது சீமென்ஸ் அலகுகளில் வெளிப்படுத்தப்படும் கட்டணத்தை நடத்துவதற்கான ஒரு பொருளின் திறனை அளவிடுகிறது.

பயன்படுத்தப்படும் வடிவியல் சார்பற்ற அளவு மின்தடையம் என்று அழைக்கப்படுகிறது மற்றும் பொதுவாக கிரேக்க சின்னமான r மூலம் குறிக்கப்படுகிறது.

கூடுதல் தகவல். ஓம் விதி மின்சார நெட்வொர்க்கின் செயல்பாட்டின் மூன்று முக்கிய குறிகாட்டிகளை நிறுவ உதவுகிறது, இது சக்தியின் கணக்கீட்டை எளிதாக்குகிறது. டையோடு, டிரான்சிஸ்டர் மற்றும் பல கூறுகளைக் கொண்ட ஒரு பக்க நெட்வொர்க்குகளுக்கு இது பொருந்தாது. மேலும் இது நேரியல் அல்லாத கூறுகளுக்குப் பொருந்தாது, இவற்றில் தைரிஸ்டர்கள் எடுத்துக்காட்டுகளாகும், ஏனெனில் இந்த உறுப்புகளின் எதிர்ப்பு மதிப்பு வெவ்வேறு கொடுக்கப்பட்ட மின்னழுத்தம் மற்றும் மின்னோட்டத்துடன் மாறுகிறது.

அதிக அதிர்வெண்களில், விநியோகிக்கப்பட்ட நடத்தை ஆதிக்கம் செலுத்துகிறது. மிக நீண்ட மின் கம்பிகளிலும் இதேதான் நடக்கிறது. 60 ஹெர்ட்ஸ் குறைவான அதிர்வெண்ணில் கூட, 30 கிமீ போன்ற மிக நீண்ட டிரான்ஸ்மிஷன் லைன் விநியோகிக்கப்பட்ட தன்மையைக் கொண்டுள்ளது.முக்கிய காரணம், சுற்றுகளில் பரவும் பயனுள்ள மின் சமிக்ஞைகள் மின்காந்த அலைகள், வோல்ட் மற்றும் ஆம்பியர்கள் அல்ல, அவை மின்காந்த அலைகளால் பாதிக்கப்படுகின்றன. கடத்திகள் வெறுமனே அலைகளுக்கு வழிகாட்டிகளாக செயல்படுகின்றன. எனவே, எடுத்துக்காட்டாக, ஒரு கோஆக்சியல் கேபிள் Z = 75 ohms ஐக் காண்பிக்கும், அதன் DC எதிர்ப்பு மிகக் குறைவாக இருந்தாலும் கூட.

ஓம் விதி என்பது மின் பொறியியலின் அடிப்படை விதி. இது அனைத்து மின்சுற்றுகள் மற்றும் மின்னணு கூறுகளிலும் அதிக எண்ணிக்கையிலான நடைமுறை பயன்பாடுகளைக் கொண்டுள்ளது.

ஓம் விதியைப் பயன்படுத்துவதற்கான பொதுவான எடுத்துக்காட்டுகள்:

1. மின்சார ஹீட்டருக்கு மின்சாரம் வழங்கப்படுகிறது. ஹீட்டர் சுருளின் எதிர்ப்பு மற்றும் பயன்படுத்தப்பட்ட மின்னழுத்தம் ஆகியவற்றைக் கொண்டு, அந்த ஹீட்டருக்கு வழங்கப்படும் சக்தியைக் கணக்கிடலாம்.
2. உருகிகளின் தேர்வு. அவை மின்னணு சாதனங்களுடன் தொடரில் இணைக்கப்பட்ட பாதுகாப்பு கூறுகள். உருகிகள்/CBகள் ஆம்ப்களில் மதிப்பிடப்படுகின்றன. தற்போதைய உருகி மதிப்பீடு ஓம் விதியைப் பயன்படுத்தி கணக்கிடப்படுகிறது.
3. மின்னணு சாதனங்களின் வடிவமைப்பு. மடிக்கணினிகள் மற்றும் மொபைல் போன்கள் போன்ற மின்னணு சாதனங்களுக்கு ஒரு குறிப்பிட்ட தற்போதைய மதிப்பீட்டுடன் DC மின்சாரம் தேவைப்படுகிறது. வழக்கமான மொபைல் ஃபோன் பேட்டரிகளுக்கு 0.7-1A தேவைப்படுகிறது. இந்த கூறுகள் வழியாக பாயும் மின்னோட்டத்தின் வீதத்தைக் கட்டுப்படுத்த மின்தடை பயன்படுத்தப்படுகிறது. ஓம் விதியானது வழக்கமான மின்னோட்டத்தில் மதிப்பிடப்பட்ட மின்னோட்டத்தைக் கணக்கிடப் பயன்படுகிறது.

ஒரு காலத்தில், ஓமின் முடிவுகள் மின்சாரத் துறையில் புதிய ஆராய்ச்சிக்கான ஊக்கியாக மாறியது, இன்று அவை அவற்றின் முக்கியத்துவத்தை இழக்கவில்லை, ஏனெனில் நவீன மின் பொறியியல் அவற்றை அடிப்படையாகக் கொண்டது. 1841 ஆம் ஆண்டில், ஓம் ராயல் சொசைட்டியின் மிக உயர்ந்த கவுரவமான கோப்லி பதக்கம் வழங்கப்பட்டது, மேலும் "ஓம்" என்ற சொல் 1872 ஆம் ஆண்டிலேயே எதிர்ப்பின் அலகாக அங்கீகரிக்கப்பட்டது.

டிசி சர்க்யூட்டின் சீரற்ற பிரிவு

ஒரு பன்முக அமைப்பு சுற்றுகளின் அத்தகைய பகுதியைக் கொண்டுள்ளது, அங்கு, கடத்திகள் மற்றும் உறுப்புகளுக்கு கூடுதலாக, தற்போதைய ஆதாரம் உள்ளது. இந்த பகுதியில் மொத்த தற்போதைய வலிமையை கணக்கிடும் போது அதன் EMF கணக்கில் எடுத்துக்கொள்ளப்பட வேண்டும்.

ஒரு பன்முக தளத்தின் முக்கிய அளவுருக்கள் மற்றும் செயல்முறைகளை வரையறுக்கும் ஒரு சூத்திரம் உள்ளது: q = q0 x n x V. அதன் குறிகாட்டிகள் பின்வருமாறு வகைப்படுத்தப்படுகின்றன:

• நகரும் கட்டணங்களின் செயல்பாட்டில் (q), அவை ஒரு குறிப்பிட்ட அடர்த்தியைப் பெறுகின்றன. அதன் செயல்திறன் தற்போதைய வலிமை மற்றும் கடத்தியின் (எஸ்) குறுக்கு வெட்டு பகுதியைப் பொறுத்தது.
• ஒரு குறிப்பிட்ட செறிவு (n) நிலைமைகளின் கீழ், ஒரே நேரத்தில் நகர்த்தப்பட்ட யூனிட் கட்டணங்களின் எண்ணிக்கையை (q0) துல்லியமாகக் குறிப்பிட முடியும்.
• கணக்கீடுகளுக்கு, கடத்தி நிபந்தனையுடன் சில தொகுதி (V) கொண்ட உருளைப் பிரிவாகக் கருதப்படுகிறது.

மின்கடத்தியை மின்கலத்துடன் இணைக்கும்போது, ​​பிந்தையது சிறிது நேரத்திற்குப் பிறகு டிஸ்சார்ஜ் செய்யப்படும். அதாவது, எலக்ட்ரான்களின் இயக்கம் படிப்படியாக குறைந்து, இறுதியில், முற்றிலும் நின்றுவிடும். மின்கடத்தியின் மூலக்கூறு லேட்டிஸால் இது எளிதாக்கப்படுகிறது, இது எலக்ட்ரான்கள் ஒன்றோடொன்று மோதுவதையும் மற்ற காரணிகளையும் எதிர்க்கிறது. அத்தகைய எதிர்ப்பைச் சமாளிக்க, சில மூன்றாம் தரப்பு சக்திகள் கூடுதலாகப் பயன்படுத்தப்பட வேண்டும்.

கணக்கீடுகளின் போது, ​​இந்த சக்திகள் கூலம்பில் சேர்க்கப்படுகின்றன. கூடுதலாக, ஒரு யூனிட் சார்ஜ் q ஐ 1 வது புள்ளியில் இருந்து 2 வது இடத்திற்கு மாற்ற, A1-2 அல்லது வெறுமனே A12 வேலை செய்ய வேண்டியது அவசியம். இந்த நோக்கத்திற்காக, சாத்தியமான வேறுபாடு (ϕ1 - ϕ2) உருவாக்கப்பட்டது. நேரடி மின்னோட்ட மூலத்தின் செயல்பாட்டின் கீழ், ஒரு EMF எழுகிறது, சுற்றுடன் கட்டணங்களை நகர்த்துகிறது. மொத்த அழுத்தத்தின் அளவு மேலே குறிப்பிடப்பட்ட அனைத்து சக்திகளையும் கொண்டிருக்கும்.

டிசி விநியோகத்திற்கான இணைப்பின் துருவமுனைப்பு கணக்கீடுகளில் கணக்கில் எடுத்துக்கொள்ளப்பட வேண்டும். டெர்மினல்கள் மாற்றப்படும் போது, ​​EMF மாறும், கட்டணங்களின் இயக்கத்தை துரிதப்படுத்தும் அல்லது மெதுவாக்கும்.

உறுப்புகளின் தொடர் மற்றும் இணை இணைப்பு

மின்சுற்றின் உறுப்புகளுக்கு (சுற்றின் பிரிவு), ஒரு சிறப்பியல்பு தருணம் ஒரு தொடர் அல்லது இணை இணைப்பு ஆகும்.

அதன்படி, ஒவ்வொரு வகை இணைப்பும் தற்போதைய ஓட்டம் மற்றும் மின்னழுத்த விநியோகத்தின் வேறுபட்ட தன்மையுடன் சேர்ந்துள்ளது. இந்தக் கணக்கில், உறுப்புகளைச் சேர்ப்பதற்கான விருப்பத்தைப் பொறுத்து, ஓம் விதியும் வெவ்வேறு வழிகளில் பயன்படுத்தப்படுகிறது.

தொடர்-இணைக்கப்பட்ட எதிர்ப்பு உறுப்புகளின் சங்கிலி

தொடர் இணைப்பைப் பொறுத்தவரை (இரண்டு கூறுகளைக் கொண்ட ஒரு சுற்றுப் பகுதி), வார்த்தைகள் பயன்படுத்தப்படுகின்றன:

• நான் = நான்₁ = ஐ₂ ;
• U = U₁ + யு₂ ;
• ஆர்=ஆர்₁ + ஆர்₂

தொடரில் இணைக்கப்பட்ட எதிர்ப்பு கூறுகளின் எண்ணிக்கையைப் பொருட்படுத்தாமல், சுற்றுகளின் ஒரு பிரிவில் பாயும் மின்னோட்டம் மதிப்பை மாற்றாது என்பதை இந்த உருவாக்கம் தெளிவாக நிரூபிக்கிறது.

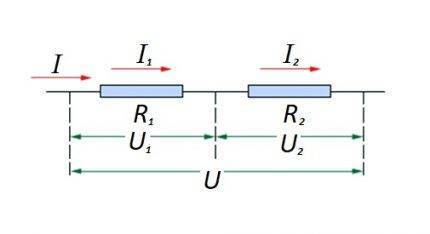மின்சுற்றுப் பிரிவில் உள்ள மின்தடை உறுப்புகளை ஒன்றோடொன்று தொடரில் இணைத்தல். இந்த விருப்பத்திற்கு அதன் சொந்த கணக்கீடு சட்டம் உள்ளது. வரைபடத்தில்: I, I1, I2 - தற்போதைய ஓட்டம்; R1, R2 - எதிர்ப்பு கூறுகள்; U, U1, U2 - பயன்படுத்தப்பட்ட மின்னழுத்தம்

மின்சுற்றின் செயலில் உள்ள மின்தடை கூறுகளுக்கு பயன்படுத்தப்படும் மின்னழுத்தத்தின் அளவு தொகை மற்றும் EMF மூலத்தின் மதிப்பை சேர்க்கிறது.

இந்த வழக்கில், ஒவ்வொரு தனிப்பட்ட கூறுகளின் மின்னழுத்தம்: Ux = I * Rx.

மொத்த எதிர்ப்பானது சுற்றுகளின் அனைத்து எதிர்ப்பு கூறுகளின் மதிப்புகளின் கூட்டுத்தொகையாக கருதப்பட வேண்டும்.

இணையாக இணைக்கப்பட்ட எதிர்ப்பு உறுப்புகளின் சங்கிலி

எதிர்ப்பு கூறுகளின் இணையான இணைப்பு இருக்கும்போது, ​​ஜெர்மன் இயற்பியலாளர் ஓமின் விதியைப் பொறுத்து உருவாக்கம் நியாயமானதாகக் கருதப்படுகிறது:

• நான் = நான்₁ + ஐ₂ … ;
• U = U₁ = யு₂ … ;
• 1/ஆர் = 1/ஆர்₁ + 1 / ஆர்₂ + …

இணையான மற்றும் தொடர் இணைப்புகளைப் பயன்படுத்தும் போது "கலப்பு" வகையின் சுற்றுப் பிரிவுகளைத் தொகுப்பதற்கான விருப்பங்கள் விலக்கப்படவில்லை.

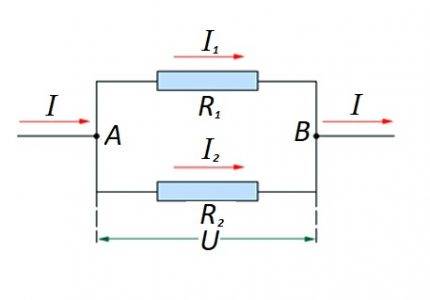ஒன்றுடன் ஒன்று இணையாக ஒரு சுற்றுப் பிரிவில் உள்ள மின்தடை உறுப்புகளின் இணைப்பு. இந்த விருப்பத்திற்கு, அதன் சொந்த கணக்கீடு சட்டம் பயன்படுத்தப்படுகிறது. வரைபடத்தில்: I, I1, I2 - தற்போதைய ஓட்டம்; R1, R2 - எதிர்ப்பு கூறுகள்; U - பயன்படுத்தப்பட்ட மின்னழுத்தம்; A, B - நுழைவு / வெளியேறும் புள்ளிகள்

அத்தகைய விருப்பங்களுக்கு, கணக்கீடு பொதுவாக இணை இணைப்பின் எதிர்ப்பு மதிப்பீட்டின் ஆரம்ப கணக்கீடு மூலம் மேற்கொள்ளப்படுகிறது. பின்னர் தொடரில் இணைக்கப்பட்ட மின்தடையத்தின் மதிப்பு முடிவில் சேர்க்கப்படுகிறது.

சட்டத்தின் ஒருங்கிணைந்த மற்றும் வேறுபட்ட வடிவங்கள்

கணக்கீடுகளுடன் மேலே உள்ள அனைத்து புள்ளிகளும் "ஒரே மாதிரியான" கட்டமைப்பின் கடத்திகள், பேசுவதற்கு, மின்சுற்றுகளின் ஒரு பகுதியாகப் பயன்படுத்தப்படும் போது நிலைமைகளுக்குப் பொருந்தும்.

இதற்கிடையில், நடைமுறையில், ஒரு திட்டவட்டமான கட்டுமானத்தை அடிக்கடி சமாளிக்க வேண்டும், அங்கு கடத்திகளின் கட்டமைப்பு வெவ்வேறு பகுதிகளில் மாறுகிறது. எடுத்துக்காட்டாக, ஒரு பெரிய குறுக்குவெட்டின் கம்பிகள் பயன்படுத்தப்படுகின்றன அல்லது மாறாக, சிறியவை வெவ்வேறு பொருட்களின் அடிப்படையில் தயாரிக்கப்படுகின்றன.

அத்தகைய வேறுபாடுகளை கணக்கில் எடுத்துக்கொள்வதற்கு, "வேறுபாடு-ஒருங்கிணைந்த ஓம் விதி" என்று அழைக்கப்படுவதில் ஒரு மாறுபாடு உள்ளது. எல்லையற்ற சிறிய கடத்திக்கு, தற்போதைய அடர்த்தி நிலை தீவிரம் மற்றும் கடத்துத்திறன் மதிப்பைப் பொறுத்து கணக்கிடப்படுகிறது.

வேறுபட்ட கணக்கீட்டின் கீழ், சூத்திரம் எடுக்கப்படுகிறது: J = ό * E

ஒருங்கிணைந்த கணக்கீட்டிற்கு, முறையே, உருவாக்கம்: I * R = φ1 - φ2 + έ

இருப்பினும், இந்த எடுத்துக்காட்டுகள் உயர் கணிதப் பள்ளிக்கு மிகவும் நெருக்கமானவை மற்றும் உண்மையில் ஒரு எளிய எலக்ட்ரீஷியனின் உண்மையான நடைமுறையில் பயன்படுத்தப்படவில்லை.

மின்னோட்டம் மற்றும் எதிர்ப்பைப் புரிந்துகொள்வது

மின்னோட்டத்தின் கருத்துடன் ஆரம்பிக்கலாம்.சுருக்கமாக, உலோகங்கள் தொடர்பாக மின்சாரம் என்பது எலக்ட்ரான்களின் இயக்கப்பட்ட இயக்கம் - எதிர்மறையாக சார்ஜ் செய்யப்பட்ட துகள்கள். அவை பொதுவாக சிறிய வட்டங்களாக குறிப்பிடப்படுகின்றன. அமைதியான நிலையில், அவர்கள் குழப்பமாக நகர்கிறார்கள், தொடர்ந்து தங்கள் திசையை மாற்றுகிறார்கள். சில நிபந்தனைகளின் கீழ் - சாத்தியமான வேறுபாட்டின் தோற்றம் - இந்த துகள்கள் சில திசையில் ஒரு குறிப்பிட்ட இயக்கத்தைத் தொடங்குகின்றன. இந்த இயக்கம் மின்சாரம்.

அதை தெளிவுபடுத்த, எலக்ட்ரான்களை சில விமானங்களில் சிந்திய தண்ணீருடன் ஒப்பிடலாம். விமானம் நிலையாக இருக்கும் வரை தண்ணீர் நகராது. ஆனால், ஒரு சாய்வு தோன்றியவுடன் (ஒரு சாத்தியமான வேறுபாடு எழுந்தது), தண்ணீர் நகரத் தொடங்கியது. எலக்ட்ரான்களும் அப்படித்தான்.

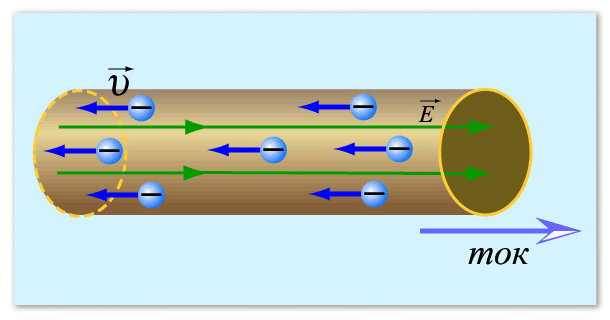
மின்னோட்டத்தை இப்படித்தான் கற்பனை செய்யலாம்

இப்போது நாம் என்ன எதிர்ப்பை புரிந்து கொள்ள வேண்டும், ஏன் அவர்கள் தற்போதைய வலிமையுடன் கருத்துக்களைக் கொண்டுள்ளனர்: அதிக எதிர்ப்பு, குறைந்த மின்னோட்டம். உங்களுக்குத் தெரியும், எலக்ட்ரான்கள் ஒரு கடத்தி வழியாக நகரும். பொதுவாக இவை உலோக கம்பிகள், உலோகங்கள் மின்சாரம் கடத்தும் நல்ல திறனைக் கொண்டிருப்பதால். உலோகம் ஒரு அடர்த்தியான படிக லேட்டிஸைக் கொண்டிருப்பதை நாம் அறிவோம்: பல துகள்கள் நெருக்கமாகவும் ஒன்றோடொன்று இணைக்கப்பட்டுள்ளன. எலக்ட்ரான்கள், உலோக அணுக்களுக்கு இடையில் தங்கள் வழியை உருவாக்கி, அவற்றுடன் மோதுகின்றன, இது அவற்றை நகர்த்துவதை கடினமாக்குகிறது. இது ஒரு கடத்தி செலுத்தும் எதிர்ப்பை விளக்க உதவுகிறது. அதிக எதிர்ப்பு, குறைந்த தற்போதைய வலிமை ஏன் இப்போது தெளிவாகிறது - அதிக துகள்கள், எலக்ட்ரான்கள் பாதையை கடப்பது மிகவும் கடினம், அவை அதை மெதுவாக செய்கின்றன. இது வரிசைப்படுத்தப்பட்டதாகத் தெரிகிறது.

இந்த சார்புநிலையை அனுபவரீதியாக சோதிக்க உங்களுக்கு விருப்பம் இருந்தால், ஒரு மாறி மின்தடையத்தைக் கண்டுபிடி, தொடரில் மின்தடையத்தை இணைக்கவும் - ஒரு அம்மீட்டர் - ஒரு தற்போதைய ஆதாரம் (பேட்டரி).சுற்றுக்குள் ஒரு சுவிட்சைச் செருகுவதும் விரும்பத்தக்கது - ஒரு சாதாரண மாற்று சுவிட்ச்.

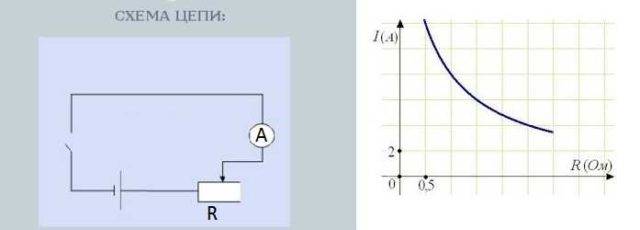
மின்னோட்ட எதிர்ப்பின் சார்புநிலையை சோதிக்கும் சுற்று

மின்தடை குமிழியைத் திருப்புவது எதிர்ப்பை மாற்றுகிறது. அதே நேரத்தில், தற்போதைய வலிமையை அளவிடும் அம்மீட்டரில் உள்ள அளவீடுகளும் மாறுகின்றன. மேலும், அதிக எதிர்ப்பு, குறைவான அம்பு விலகுகிறது - குறைந்த மின்னோட்டம். குறைந்த எதிர்ப்பு, மேலும் அம்பு விலகுகிறது - தற்போதைய அதிகமாக உள்ளது.

எதிர்ப்பின் மீதான மின்னோட்டத்தின் சார்பு கிட்டத்தட்ட நேரியல் ஆகும், அதாவது, இது வரைபடத்தில் கிட்டத்தட்ட நேர் கோடாக பிரதிபலிக்கிறது. ஏன் கிட்டத்தட்ட - இது தனித்தனியாக விவாதிக்கப்பட வேண்டும், ஆனால் அது மற்றொரு கதை.

மாற்று மின்னோட்டத்திற்கான ஓம் விதி

ஏசி சர்க்யூட்களை கணக்கிடும் போது, ​​எதிர்ப்பின் கருத்துக்கு பதிலாக, "மின்மறுப்பு" என்ற கருத்து அறிமுகப்படுத்தப்படுகிறது. மின்மறுப்பு என்பது Z என்ற எழுத்தால் குறிக்கப்படுகிறது, இது சுமை R இன் செயலில் உள்ள எதிர்ப்பை உள்ளடக்கியது_அ மற்றும் எதிர்வினை X (அல்லது ஆர்_ஆர்) இது சைனூசாய்டல் மின்னோட்டத்தின் வடிவம் (மற்றும் வேறு எந்த வடிவங்களின் நீரோட்டங்கள்) மற்றும் தூண்டல் உறுப்புகளின் அளவுருக்கள் மற்றும் மாறுதல் விதிகள் காரணமாகும்:

1. ஒரு தூண்டல் சுற்று மின்னோட்டத்தை உடனடியாக மாற்ற முடியாது.
2. கொள்ளளவு கொண்ட மின்சுற்றில் உள்ள மின்னழுத்தம் உடனடியாக மாற முடியாது.

இதனால், மின்னோட்டம் பின்தங்கிய அல்லது மின்னழுத்தத்தை வழிநடத்தத் தொடங்குகிறது, மேலும் வெளிப்படையான சக்தி செயலில் மற்றும் எதிர்வினையாக பிரிக்கப்படுகிறது.

U=I/Z

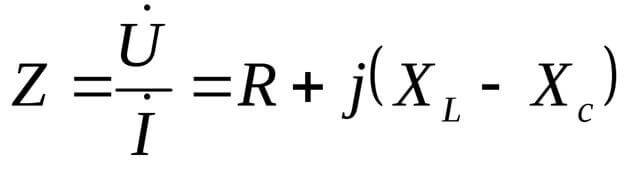
எக்ஸ்_எல் மற்றும் எக்ஸ்_சி சுமையின் எதிர்வினை கூறுகளாகும்.

இது சம்பந்தமாக, மதிப்பு cosФ அறிமுகப்படுத்தப்பட்டது:

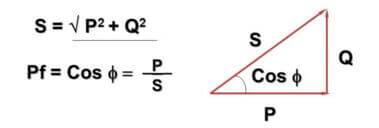
இங்கே - Q - மாற்று மின்னோட்டம் மற்றும் தூண்டல்-கொள்திறன் கூறுகள் காரணமாக எதிர்வினை சக்தி, P - செயலில் சக்தி (செயலில் உள்ள கூறுகளில் சிதறியது), S - வெளிப்படையான சக்தி, cosФ - சக்தி காரணி.

சூத்திரமும் அதன் பிரதிநிதித்துவமும் பித்தகோரியன் தேற்றத்துடன் குறுக்கிடுவதை நீங்கள் கவனித்திருக்கலாம். இது உண்மை மற்றும் கோணம் Ф சுமையின் எதிர்வினை கூறு எவ்வளவு பெரியது என்பதைப் பொறுத்தது - அது பெரியது, பெரியது.நடைமுறையில், நெட்வொர்க்கில் உண்மையில் பாயும் மின்னோட்டம் ஒரு வீட்டு மீட்டரால் கணக்கில் எடுத்துக்கொள்ளப்பட்டதை விட அதிகமாக உள்ளது என்பதற்கு இது வழிவகுக்கிறது, அதே நேரத்தில் நிறுவனங்கள் முழு சக்தியையும் செலுத்துகின்றன.

இந்த வழக்கில், எதிர்ப்பு சிக்கலான வடிவத்தில் வழங்கப்படுகிறது:

இங்கே j என்பது ஒரு கற்பனை அலகு, இது சமன்பாடுகளின் சிக்கலான வடிவத்திற்கு பொதுவானது. குறைவாக பொதுவாக i என குறிப்பிடப்படுகிறது, ஆனால் மின் பொறியியலில், மாற்று மின்னோட்டத்தின் பயனுள்ள மதிப்பும் குறிக்கப்படுகிறது, எனவே, குழப்பமடையாமல் இருக்க, j ஐப் பயன்படுத்துவது நல்லது.

கற்பனை அலகு √-1. ஸ்கொயர் செய்யும் போது அத்தகைய எண் இல்லை என்பது தர்க்கரீதியானது, இது "-1" இன் எதிர்மறையான முடிவை ஏற்படுத்தும்.

ஓம் விதி ஏற்படும் போது

சிறந்த நிலைமைகளை உருவாக்குவது எளிதானது அல்ல. தூய கடத்திகளில் கூட, மின் எதிர்ப்பு வெப்பநிலையுடன் மாறுபடும். அதன் குறைவு படிக லட்டியின் மூலக்கூறுகளின் செயல்பாட்டைக் குறைக்கிறது, இது இலவச கட்டணங்களின் இயக்கத்தை எளிதாக்குகிறது. "உறைபனி" ஒரு குறிப்பிட்ட அளவில் சூப்பர் கண்டக்டிவிட்டி விளைவு ஏற்படுகிறது. சூடான போது எதிர் விளைவு (கடத்துத்திறன் சரிவு) காணப்படுகிறது.

அதே நேரத்தில், எலக்ட்ரோலைட்டுகள், உலோகங்கள் மற்றும் சில வகையான மட்பாண்டங்கள் தற்போதைய அடர்த்தியைப் பொருட்படுத்தாமல் மின் எதிர்ப்பைத் தக்கவைத்துக்கொள்கின்றன. ஒரு குறிப்பிட்ட வெப்பநிலை ஆட்சியை பராமரிக்கும் போது அளவுருக்களின் ஸ்திரத்தன்மை கூடுதல் திருத்தங்கள் இல்லாமல் ஓம் சட்டத்தின் சூத்திரங்களைப் பயன்படுத்துவதை சாத்தியமாக்குகிறது.

குறைக்கடத்தி பொருட்கள் மற்றும் வாயுக்கள் பல்வேறு மின் எதிர்ப்பால் வகைப்படுத்தப்படுகின்றன. இந்த அளவுரு கட்டுப்பாட்டு தொகுதியின் தற்போதைய தீவிரத்தால் கணிசமாக பாதிக்கப்படுகிறது. செயல்திறன் பண்புகளை கணக்கிட, சிறப்பு கணக்கீட்டு முறைகள் பயன்படுத்தப்பட வேண்டும்.

மாற்று மின்னோட்டம் கருதப்பட்டால், கணக்கீட்டு முறை சரி செய்யப்படுகிறது.இந்த வழக்கில், எதிர்வினை கூறுகளின் இருப்பு கணக்கில் எடுத்துக்கொள்ளப்பட வேண்டும். எதிர்ப்பின் எதிர்ப்பு தன்மையுடன், ஓம் விதியின் சூத்திரங்களின் அடிப்படையில் கருதப்படும் கணக்கீட்டு தொழில்நுட்பங்களைப் பயன்படுத்துவது சாத்தியமாகும்.

கிர்ச்சாஃப் சட்டங்கள்.

விநியோகம்
மின்சுற்றின் கிளைகளில் நீரோட்டங்கள்
Kirchhoff இன் முதல் சட்டத்திற்கு கீழ்ப்படிகிறது,
மற்றும் பிரிவுகளின் மீது அழுத்தங்களின் விநியோகம்
சங்கிலி கிர்ச்சாஃப்பின் இரண்டாவது விதிக்கு கீழ்ப்படிகிறது.

கிர்ச்சாஃப் சட்டங்கள்
ஓம் விதியுடன் சேர்த்து முக்கியமானது
மின்சுற்றுகளின் கோட்பாட்டில்.

முதலாவதாக
Kirchhoff சட்டம்:

இயற்கணிதம்
முனையிலுள்ள மின்னோட்டங்களின் கூட்டுத்தொகை பூஜ்ஜியம்:

_நான்
= 0 (19)

எங்கே
நான்
கொடுக்கப்பட்ட முனையில் ஒன்றிணைக்கும் கிளைகளின் எண்ணிக்கை.

அதாவது, கூட்டுத்தொகை
கிளைகளில் நீரோட்டங்கள் வரை நீண்டுள்ளது,
கருதப்பட்டதில் சங்கமிக்கும்
முனை.

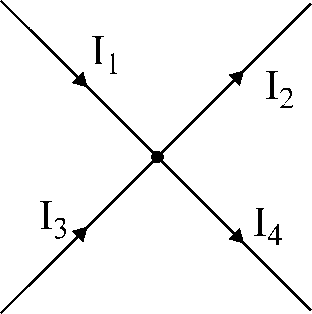
படம்.17. விளக்கம்
Kirchhoff இன் முதல் சட்டத்திற்கு.

எண்
முதல் படி தொகுக்கப்பட்ட சமன்பாடுகள்
கிர்ச்சோஃப் விதி சூத்திரத்தால் தீர்மானிக்கப்படுகிறது:

Nup
= நு
– 1,

எங்கே
நு
கருதப்படும் சங்கிலியில் உள்ள முனைகளின் எண்ணிக்கை.

மின்னோட்டத்தின் அறிகுறிகள்
தேர்ந்தெடுக்கப்பட்டதை கணக்கில் எடுத்துக்கொண்டு சமன்பாடுகள் எடுக்கப்படுகின்றன
நேர்மறை திசை. இல் அடையாளங்கள்
நீரோட்டங்கள் ஒரே மாதிரியாக இருந்தால் ஒரே மாதிரியாக இருக்கும்
இதனுடன் தொடர்புடையது
முனை.

உதாரணத்திற்கு,
படம் 17 இல் காட்டப்பட்டுள்ள முனைக்கு:
முனையில் பாயும் நீரோட்டங்களுக்கு அடையாளங்களை ஒதுக்குகிறோம்
"+", மற்றும் முனையிலிருந்து பாயும் நீரோட்டங்களுக்கு - அறிகுறிகள்
«-».

பிறகு சமன்பாடு
Kirchhoff இன் முதல் சட்டத்தின்படி, அது எழுதப்படும்
அதனால்:

நான்₁
- நான்₂
+ ஐ₃
- நான்₄
= 0.

சமன்பாடுகள்,
Kirchhoff இன் முதல் சட்டத்தின்படி தொகுக்கப்பட்டது,
முனைகள் என்று அழைக்கப்படுகின்றன.

இது
சட்டம் முனையில் என்ற உண்மையை வெளிப்படுத்துகிறது
மின்சார கட்டணம் குவிவதில்லை
மற்றும் நுகரப்படவில்லை. மின் அளவு
தளத்திற்கு வரும் கட்டணங்கள் தொகைக்கு சமம்
ஒரே ஒரு முனையில் இருந்து கட்டணங்கள்
அதே கால அளவு.

இரண்டாவது
Kirchhoff சட்டம்:

இயற்கணிதம்
emf இன் தொகை எந்த மூடிய சுற்றுகளிலும்
சங்கிலி நீர்வீழ்ச்சியின் இயற்கணிதத் தொகைக்கு சமம்
இந்த சுற்று உறுப்புகளில் மின்னழுத்தம்:

உய்
= 
ஈ

IiRi=Ei(20)

எங்கே
நான்
- உறுப்பு எண் (எதிர்ப்பு அல்லது
மின்னழுத்த ஆதாரம்) கருதப்படுகிறது
விளிம்பு.

**எண்
இரண்டாவது படி தொகுக்கப்பட்ட சமன்பாடுகள்
கிர்ச்சோஃப் விதி சூத்திரத்தால் தீர்மானிக்கப்படுகிறது:

Nup
= Nb
- நு
+ 1 – Ned.s.

எங்கே
Nb
- மின்சுற்றின் கிளைகளின் எண்ணிக்கை;

நு
- முனைகளின் எண்ணிக்கை;

நெட்.எஸ்.
சிறந்த emf ஆதாரங்களின் எண்ணிக்கை.

படம்.18. விளக்கம்
Kirchhoff இன் இரண்டாவது விதிக்கு.

இதற்கு,
இரண்டாவது சட்டத்தை சரியாக எழுத வேண்டும்
கொடுக்கப்பட்ட விளிம்பிற்கு கிர்ச்சோஃப் பின்வருமாறு
பின்வரும் விதிகளுக்கு இணங்க:

1. தன்னிச்சையாக
   விளிம்பு பைபாஸின் திசையைத் தேர்ந்தெடுக்கவும்,
   உதாரணமாக, கடிகார திசையில் (படம் 18).

2. emf
   மற்றும் மின்னழுத்தம் குறைகிறது
   தேர்ந்தெடுக்கப்பட்ட திசையுடன் திசையில்
   பைபாஸ் உடன் ஒரு வெளிப்பாட்டில் எழுதப்பட்டுள்ளது
   அடையாளம் "+"; e.f.s என்றால். மற்றும் மின்னழுத்த வீழ்ச்சி
   திசையில் பொருந்தவில்லை
   விளிம்பு, பின்னர் அவர்கள் ஒரு அடையாளம் மூலம் முன்
   «-».

உதாரணத்திற்கு,
படம் 18 இன் விளிம்பிற்கு, கிர்ச்சாஃப்பின் இரண்டாவது விதி
பின்வருமாறு எழுதப்படும்:

யு₁
– யு₂
+ யு₃
= ஈ₁
– ஈ₃
– ஈ₄
(21)

சமன்பாடு (20) இருக்கலாம்
இவ்வாறு மீண்டும் எழுதவும்:

 (Ui
– ஈ)
= 0 (22)

எங்கே
(யு
– இ)
- கிளையில் பதற்றம்.

இதன் விளைவாக,
கிர்ச்சாஃப்பின் இரண்டாவது விதியை உருவாக்கலாம்
பின்வரும் வழியில்:

இயற்கணிதம்
கிளைகளில் உள்ள மின்னழுத்தங்களின் கூட்டுத்தொகை
மூடிய வளையம் பூஜ்ஜியமாகும்.

சாத்தியமான
முன்னர் விவாதிக்கப்பட்ட வரைபடம் உதவுகிறது
இரண்டாவது வரைகலை விளக்கம்
Kirchhoff சட்டம்.

பணி எண் 1.

AT
படம் 1 இல் உள்ள சுற்றுக்கு மின்னோட்டங்கள் I கொடுக்கப்பட்டுள்ளது₁
மற்றும் நான்₃,
எதிர்ப்பு மற்றும் emf நீரோட்டங்களைத் தீர்மானிக்கவும்
நான்₄,
நான்₅,
நான்₆
; புள்ளிகளுக்கு இடையே மின்னழுத்தம் a
மற்றும் பி
ஒருவேளை நான்₁
= 10mA,
நான்₃
= -20 mA,
ஆர்₄
= 5kOhm,
ஈ₅
= 20B,
ஆர்₅
= 3kOhm,
ஈ₆
= 40B,
ஆர்₆
= 2kOhm.

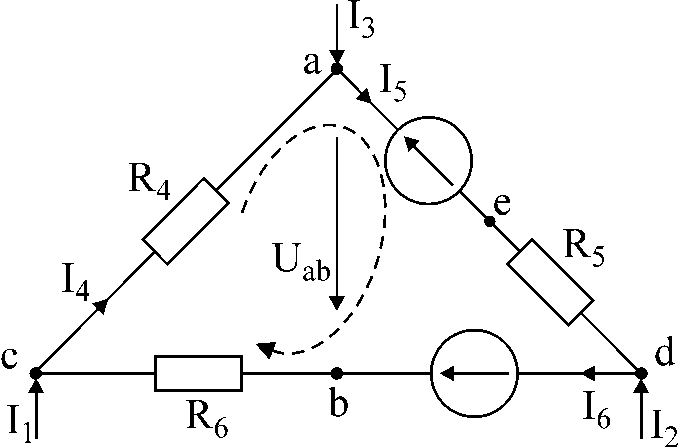
வரைபடம். 1

தீர்வு:

1. கொடுக்கப்பட்டதற்கு
   விளிம்பு, அதன்படி இரண்டு சமன்பாடுகளை உருவாக்குகிறோம்
   Kirchhoff இன் முதல் சட்டம் மற்றும் ஒன்று - படி
   இரண்டாவது. விளிம்பு திசை
   ஒரு அம்புக்குறி மூலம் சுட்டிக்காட்டப்படுகிறது.

AT
தீர்வின் விளைவாக நாம் பெறுகிறோம்: I₆
= 0; நான்₄
= 10mA;
நான்₅
= -10mA

1. கேட்க
   புள்ளிகளுக்கு இடையே மின்னழுத்த திசை
   அ
   மற்றும் பி
   புள்ளி "a" இலிருந்து
   புள்ளி "b"
   - யு_ab.
   இந்த மின்னழுத்தத்தை சமன்பாட்டிலிருந்து காணலாம்
   Kirchhoff இன் இரண்டாவது விதி:

நான்₄ஆர்₄
+ யு_ab
+ ஐ₆ஆர்₆
= 0

யு_ab
= - 50V.

பணி எண் 2.

க்கு
படம் 2 இல் உள்ள வரைபடங்கள் படி சமன்பாடுகளை வரைகின்றன
Kirchhoff சட்டங்கள் மற்றும் தெரியாதவற்றை தீர்மானிக்கின்றன
புள்ளிகள்.

கொடுக்கப்பட்டது:
நான்₁
= 20mA;
நான்₂
= 10mA

ஆர்₁
= 5kOhm,
ஆர்₃
= 4kOhm,
ஆர்₄
= 6kOhm,
ஆர்₅
= 2kOhm,
ஆர்₆
= 4kΩ.

படம்.2

தீர்வு:

முனைகளின் எண்ணிக்கை
சமன்பாடுகள் - 3, விளிம்பு சமன்பாடுகளின் எண்ணிக்கை
– 1.

நினைவில் கொள்ளுங்கள்!
இரண்டாவது படி சமன்பாட்டை தொகுக்கும்போது
Kirchhoff விதி, நாங்கள் விளிம்பை தேர்வு செய்கிறோம்
இதில் தற்போதைய ஆதாரங்கள் இல்லை.
விளிம்பின் திசை படத்தில் சுட்டிக்காட்டப்பட்டுள்ளது.

AT
இந்த சுற்று, கிளைகளின் நீரோட்டங்கள் I₁
மற்றும் நான்₂.
தெரியவில்லை
நீரோட்டங்கள்
நான்₃,
நான்₄,
நான்₅,
நான்₆.

தீர்மானிக்கிறது
அமைப்பு, நாம் பெறுகிறோம்: I₃
= 13.75 mA;
நான்₄
= -3.75mA;
நான்₅
= 6.25mA;
நான்₆
= 16.25mA

அடிப்படை கருத்துக்கள்

ஒரு மூடிய சுற்று எலக்ட்ரான்களை அதிக ஆற்றலில் இருந்து குறைந்த சுற்றுக்கு நகர்த்த அனுமதிக்கும் போது மின்சாரம் பாய்கிறது. வேறு வார்த்தைகளில் கூறுவதானால், மின்னோட்டத்திற்கு எலக்ட்ரான்களின் ஆதாரம் தேவைப்படுகிறது, அவை அவற்றை இயக்கத்தில் அமைக்கும் ஆற்றலைக் கொண்டுள்ளன, அதே போல் எதிர்மறைக் கட்டணங்களைத் திரும்பப் பெறும் புள்ளியும் அவற்றின் குறைபாட்டால் வகைப்படுத்தப்படுகிறது. ஒரு இயற்பியல் நிகழ்வாக, ஒரு சுற்றுவட்டத்தின் மின்னோட்டம் மூன்று அடிப்படை அளவுகளால் வகைப்படுத்தப்படுகிறது:

• மின்னழுத்தம்;
• தற்போதைய வலிமை;
• எலக்ட்ரான்கள் நகரும் கடத்தியின் எதிர்ப்பு.

வலிமை மற்றும் பதற்றம்

மின்னோட்ட வலிமை (I, ஆம்பியர்ஸில் அளவிடப்படுகிறது) என்பது ஒரு யூனிட் நேரத்திற்கு மின்சுற்றில் ஒரு இடத்தில் நகரும் எலக்ட்ரான்களின் (சார்ஜ்) அளவு ஆகும்.வேறு வார்த்தைகளில் கூறுவதானால், அளவீடு I என்பது இயக்கத்தில் உள்ள எலக்ட்ரான்களின் எண்ணிக்கையை தீர்மானிப்பதாகும்

இந்த சொல் இயக்கத்தை மட்டுமே குறிக்கிறது என்பதை புரிந்து கொள்ள வேண்டியது அவசியம்: நிலையான கட்டணங்கள், எடுத்துக்காட்டாக, இணைக்கப்படாத பேட்டரியின் முனையங்களில், I இன் அளவிடக்கூடிய மதிப்பு இல்லை. ஒரு திசையில் பாயும் மின்னோட்டம் நேரடி (DC) என அழைக்கப்படுகிறது, மேலும் அவ்வப்போது மாறும் திசையை மாற்று (ஏசி) என்று அழைக்கப்படுகிறது. மின்னழுத்தத்தை அழுத்தம் போன்ற ஒரு நிகழ்வு அல்லது புவியீர்ப்பு செல்வாக்கின் கீழ் உள்ள பொருட்களின் சாத்தியமான ஆற்றலில் உள்ள வேறுபாடு மூலம் விளக்கலாம்.

இந்த ஏற்றத்தாழ்வை உருவாக்க, நீங்கள் முதலில் ஆற்றலைச் செலவிட வேண்டும், இது பொருத்தமான சூழ்நிலையில் இயக்கத்தில் உணரப்படும். எடுத்துக்காட்டாக, உயரத்திலிருந்து ஒரு சுமை வீழ்ச்சியடையும் போது, ​​​​அதை தூக்கும் பணி மேற்கொள்ளப்படுகிறது, கால்வனிக் பேட்டரிகளில், டெர்மினல்களில் சாத்தியமான வேறுபாடு இரசாயன ஆற்றலை மாற்றுவதன் காரணமாக, ஜெனரேட்டர்களில் - வெளிப்பாட்டின் விளைவாக உருவாகிறது. ஒரு மின்காந்த புலம்

அழுத்தம் போன்ற ஒரு நிகழ்வு அல்லது புவியீர்ப்பு செல்வாக்கின் கீழ் உள்ள பொருட்களின் சாத்தியமான ஆற்றலில் உள்ள வேறுபாடு போன்ற ஒரு நிகழ்வால் மன அழுத்தத்தை விளக்கலாம். இந்த ஏற்றத்தாழ்வை உருவாக்க, நீங்கள் முதலில் ஆற்றலைச் செலவிட வேண்டும், இது பொருத்தமான சூழ்நிலையில் இயக்கத்தில் உணரப்படும். எடுத்துக்காட்டாக, உயரத்திலிருந்து ஒரு சுமை வீழ்ச்சியடையும் போது, ​​​​அதைத் தூக்கும் வேலை உணரப்படுகிறது, கால்வனிக் பேட்டரிகளில், ரசாயன ஆற்றலின் மாற்றத்தால் டெர்மினல்களில் சாத்தியமான வேறுபாடு உருவாகிறது, ஜெனரேட்டர்களில் - ஒரு வெளிப்பாட்டின் விளைவாக. மின்காந்த புலம்.

கடத்தி எதிர்ப்பு

ஒரு சாதாரண கடத்தி எவ்வளவு சிறந்ததாக இருந்தாலும், எலக்ட்ரான்கள் அவற்றின் இயக்கத்திற்கு எதிர்ப்பு இல்லாமல் கடந்து செல்ல அனுமதிக்காது.எதிர்ப்பை இயந்திர உராய்வின் அனலாக் என்று கருதுவது சாத்தியம், இருப்பினும் இந்த ஒப்பீடு சரியானதாக இருக்காது. ஒரு கடத்தி வழியாக மின்னோட்டம் பாயும் போது, ​​சில சாத்தியமான வேறுபாடு வெப்பமாக மாற்றப்படுகிறது, எனவே மின்தடையில் எப்போதும் மின்னழுத்த வீழ்ச்சி இருக்கும். மின்சார ஹீட்டர்கள், முடி உலர்த்திகள் மற்றும் பிற ஒத்த சாதனங்கள் வெப்ப வடிவில் மின் ஆற்றலைச் சிதறடிக்க மட்டுமே வடிவமைக்கப்பட்டுள்ளன.

எளிமைப்படுத்தப்பட்ட எதிர்ப்பு (ஆர் என குறிப்பிடப்படுகிறது) என்பது ஒரு மின்சுற்றில் எலக்ட்ரான்களின் ஓட்டம் எவ்வளவு தாமதமாகிறது என்பதற்கான அளவீடு ஆகும். இது ஓம்ஸில் அளவிடப்படுகிறது. மின்தடை அல்லது பிற தனிமத்தின் கடத்துத்திறன் இரண்டு பண்புகளால் தீர்மானிக்கப்படுகிறது:

• வடிவியல்;
• பொருள்.

ஹைட்ராலிக் ஒப்புமையிலிருந்து தெளிவாகத் தெரிகிறது, வடிவம் மிக முக்கியமானது: நீண்ட மற்றும் குறுகிய குழாய் வழியாக தண்ணீரைத் தள்ளுவது குறுகிய மற்றும் அகலமான வழியாக தண்ணீரைத் தள்ளுவதை விட மிகவும் கடினமானது. பொருட்கள் ஒரு தீர்க்கமான பாத்திரத்தை வகிக்கின்றன. எடுத்துக்காட்டாக, எலக்ட்ரான்கள் ஒரு செப்பு கம்பியில் சுதந்திரமாக நகர முடியும், ஆனால் அவற்றின் வடிவத்தைப் பொருட்படுத்தாமல் ரப்பர் போன்ற மின்கடத்திகள் வழியாகப் பாய முடியாது. வடிவியல் மற்றும் பொருள் தவிர, கடத்துத்திறனை பாதிக்கும் பிற காரணிகளும் உள்ளன.

ஓமின் சட்ட விளக்கம்

கட்டணங்களின் இயக்கத்தை உறுதிப்படுத்த, நீங்கள் சுற்று மூட வேண்டும். கூடுதல் மின்சாரம் இல்லாத நிலையில், மின்னோட்டம் நீண்ட நேரம் இருக்க முடியாது. வாய்ப்புகள் விரைவில் சமமாகிவிடும். சுற்று இயக்க முறைமையை பராமரிக்க, கூடுதல் ஆதாரம் (ஜெனரேட்டர், பேட்டரி) தேவை.

முழுமையான சுற்று அனைத்து கூறுகளின் மொத்த மின் எதிர்ப்பைக் கொண்டிருக்கும். துல்லியமான கணக்கீடுகளுக்கு, கடத்திகள், எதிர்ப்பு கூறுகள் மற்றும் ஒரு சக்தி மூலத்தில் ஏற்படும் இழப்புகள் கணக்கில் எடுத்துக்கொள்ளப்படுகின்றன.

ஒரு குறிப்பிட்ட மின்னோட்ட வலிமைக்கு எவ்வளவு மின்னழுத்தம் பயன்படுத்தப்பட வேண்டும் என்பது சூத்திரத்தால் கணக்கிடப்படுகிறது:

U=I*R.

இதேபோல், கருதப்பட்ட உறவுகளின் உதவியுடன், சுற்றுகளின் மற்ற அளவுருக்கள் தீர்மானிக்கப்படுகின்றன.

இணை மற்றும் தொடர் இணைப்பு

எலக்ட்ரிக்ஸில், உறுப்புகள் தொடரில் இணைக்கப்படுகின்றன - ஒன்றன் பின் ஒன்றாக, அல்லது இணையாக - பல உள்ளீடுகள் ஒரு புள்ளியுடன் இணைக்கப்படும் போது, ​​அதே உறுப்புகளின் வெளியீடுகள் மற்றொன்றுடன் இணைக்கப்படும்.

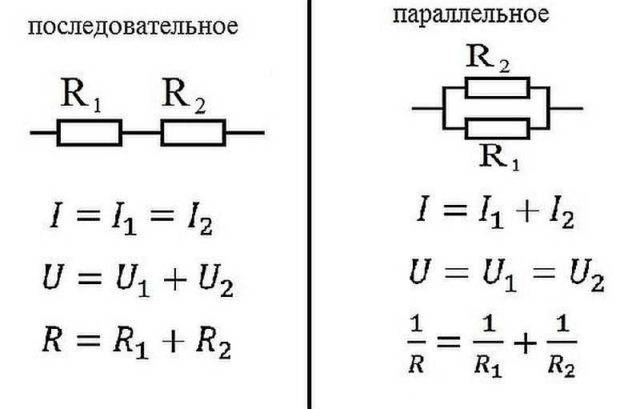
இணை மற்றும் தொடர் இணைப்புக்கான ஓம் விதி

தொடர் இணைப்பு

இந்த வழக்குகளுக்கு ஓமின் சட்டம் எவ்வாறு செயல்படுகிறது? தொடரில் இணைக்கப்படும் போது, ​​உறுப்புகளின் சங்கிலி வழியாக பாயும் மின்னோட்டம் ஒரே மாதிரியாக இருக்கும். தொடரில் இணைக்கப்பட்ட உறுப்புகளைக் கொண்ட ஒரு சுற்றுப் பிரிவின் மின்னழுத்தம் ஒவ்வொரு பிரிவிலும் உள்ள மின்னழுத்தங்களின் கூட்டுத்தொகையாகக் கணக்கிடப்படுகிறது. இதை எப்படி விளக்க முடியும்? ஒரு உறுப்பு வழியாக மின்னோட்டத்தின் ஓட்டம் என்பது அதன் ஒரு பகுதியிலிருந்து மற்றொரு பகுதிக்கு கட்டணத்தின் ஒரு பகுதியை மாற்றுவதாகும். அதாவது, இது ஏதோ வேலை. இந்த வேலையின் அளவு பதற்றம். இது மன அழுத்தத்தின் உடல் பொருள். இது தெளிவாக இருந்தால், நாங்கள் தொடர்கிறோம்.

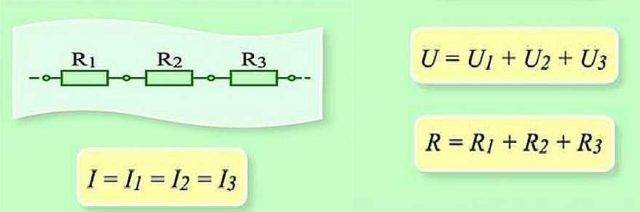
சர்க்யூட்டின் இந்த பிரிவின் தொடர் இணைப்பு மற்றும் அளவுருக்கள்

தொடரில் இணைக்கப்படும் போது, ​​ஒவ்வொரு உறுப்பு வழியாகவும் கட்டணத்தை மாற்றுவது அவசியம். ஒவ்வொரு உறுப்புக்கும், இது ஒரு குறிப்பிட்ட "தொகுதி" வேலை. சங்கிலியின் முழுப் பகுதியிலும் வேலையின் அளவைக் கண்டுபிடிக்க, ஒவ்வொரு உறுப்புக்கும் வேலை சேர்க்க வேண்டும். எனவே மொத்த மின்னழுத்தம் என்பது ஒவ்வொரு உறுப்புகளின் மின்னழுத்தங்களின் கூட்டுத்தொகை என்று மாறிவிடும்.

அதே வழியில் - கூடுதலாக உதவியுடன் - சுற்று பிரிவின் மொத்த எதிர்ப்பும் காணப்படுகிறது. நீங்கள் அதை எப்படி கற்பனை செய்ய முடியும்? உறுப்புகளின் சங்கிலி வழியாக பாயும் மின்னோட்டம் தொடர்ச்சியாக அனைத்து எதிர்ப்புகளையும் கடக்கிறது. ஒவ்வொன்றாக. அதாவது, அவர் முறியடித்த எதிர்ப்பைக் கண்டுபிடிக்க, எதிர்ப்புகளைச் சேர்க்க வேண்டியது அவசியம். அதிகமாகவோ அல்லது குறைவாகவோ இப்படி.கணித வழித்தோன்றல் மிகவும் சிக்கலானது, மேலும் இந்த சட்டத்தின் பொறிமுறையைப் புரிந்துகொள்வது எளிது.

இணை இணைப்பு

ஒரு இணையான இணைப்பு என்பது கடத்திகள் / உறுப்புகளின் தொடக்கங்கள் ஒரு கட்டத்தில் ஒன்றிணைந்து, மற்றொரு கட்டத்தில் அவற்றின் முனைகள் இணைக்கப்படும் போது. இந்த வகை கலவைகளுக்கு செல்லுபடியாகும் சட்டங்களை விளக்க முயற்சிப்போம். மின்னோட்டத்துடன் ஆரம்பிக்கலாம். உறுப்புகளின் இணைப்புப் புள்ளியில் சில அளவு மின்னோட்டம் வழங்கப்படுகிறது. இது பிரிக்கிறது, அனைத்து கடத்திகள் வழியாக பாய்கிறது. இதிலிருந்து பிரிவின் மொத்த மின்னோட்டமானது ஒவ்வொரு உறுப்புகளிலும் உள்ள மின்னோட்டத்தின் கூட்டுத்தொகைக்கு சமம் என்று முடிவு செய்கிறோம்: I = I1 + I2 + I3.

இப்போது மின்னழுத்தத்திற்கு. மின்னழுத்தம் ஒரு கட்டணத்தை நகர்த்துவதற்கான வேலை எனில், ஒரு கட்டணத்தை நகர்த்துவதற்குத் தேவைப்படும் வேலை எந்த உறுப்புக்கும் ஒரே மாதிரியாக இருக்கும். அதாவது, இணையாக இணைக்கப்பட்ட ஒவ்வொரு உறுப்புக்கும் உள்ள மின்னழுத்தம் ஒரே மாதிரியாக இருக்கும். U=U1=U2=U3. ஒரு சங்கிலிப் பிரிவிற்கு ஓம் விதியின் விளக்கத்தைப் போல வேடிக்கையாகவும் காட்சியாகவும் இல்லை, ஆனால் நீங்கள் புரிந்து கொள்ள முடியும்.

இணை இணைப்புக்கான சட்டங்கள்

எதிர்ப்பைப் பொறுத்தவரை, விஷயங்கள் சற்று சிக்கலானவை. கடத்துத்திறன் என்ற கருத்தை அறிமுகப்படுத்துவோம். இந்த கடத்தியின் வழியாக கட்டணம் செலுத்துவது எவ்வளவு எளிதானது அல்லது கடினம் என்பதைக் குறிக்கும் பண்பு இதுவாகும். மின்தடை குறைவாக இருந்தால், மின்னோட்டத்தை கடந்து செல்வது எளிதாக இருக்கும் என்பது தெளிவாகிறது. எனவே, கடத்துத்திறன் - ஜி - எதிர்ப்பின் பரஸ்பரமாக கணக்கிடப்படுகிறது. சூத்திரத்தில், இது போல் தெரிகிறது: G = 1/R.

கடத்துத்திறன் பற்றி நாம் ஏன் பேசுகிறோம்? ஏனெனில் தனிமங்களின் இணையான இணைப்பு கொண்ட ஒரு பிரிவின் மொத்த கடத்துத்திறன் ஒவ்வொரு பிரிவின் கடத்துத்திறனின் கூட்டுத்தொகைக்கு சமம். G = G1 + G2 + G3 - புரிந்துகொள்ள எளிதானது. இணையான தனிமங்களின் இந்த முனையை மின்னோட்டம் எவ்வளவு எளிதில் கடக்கும் என்பது ஒவ்வொரு தனிமங்களின் கடத்துத்திறனைப் பொறுத்தது. எனவே அவை மடிக்கப்பட வேண்டும் என்று மாறிவிடும்.

இப்போது நாம் எதிர்ப்பிற்கு செல்லலாம்.கடத்துத்திறன் எதிர்ப்பின் பரஸ்பரம் என்பதால், நாம் பின்வரும் சூத்திரத்தைப் பெறலாம்: 1/R = 1/R1 + 1/R2 + 1/R3.

நமக்கு இணையான மற்றும் தொடர் இணைப்பை எது தருகிறது?

கோட்பாட்டு அறிவு நல்லது, ஆனால் அதை நடைமுறையில் எவ்வாறு பயன்படுத்துவது? எந்த வகை கூறுகளையும் இணையாகவும் தொடராகவும் இணைக்க முடியும். ஆனால் நேரியல் கூறுகளை விவரிக்கும் எளிய சூத்திரங்களை மட்டுமே நாங்கள் கருதினோம். நேரியல் கூறுகள் எதிர்ப்புகள், அவை "எதிர்ப்புகள்" என்றும் அழைக்கப்படுகின்றன. எனவே நீங்கள் கற்றுக்கொண்டதை எவ்வாறு பயன்படுத்தலாம் என்பது இங்கே:

பெரிய மதிப்பு மின்தடையம் இல்லை, ஆனால் பல சிறிய மின்தடையங்கள் இருந்தால், தொடரில் பல மின்தடையங்களை இணைப்பதன் மூலம் விரும்பிய எதிர்ப்பைப் பெறலாம். நீங்கள் பார்க்க முடியும் என, இது ஒரு பயனுள்ள தந்திரம்.
பேட்டரிகளின் ஆயுளை நீட்டிக்க, அவை இணையாக இணைக்கப்படலாம். இந்த வழக்கில், ஓம் விதியின்படி மின்னழுத்தம் அப்படியே இருக்கும் (மல்டிமீட்டருடன் மின்னழுத்தத்தை அளவிடுவதன் மூலம் நீங்கள் உறுதிசெய்யலாம்). இரட்டை பேட்டரியின் "வாழ்நாள்" இரண்டு கூறுகளை விட அதிகமாக இருக்கும், அவை ஒன்றையொன்று மாற்றும்

கவனிக்கவும்: ஒரே ஆற்றல் கொண்ட மின்சாரம் மட்டுமே இணையாக இணைக்கப்படும். அதாவது, ஒரு இறந்த மற்றும் புதிய பேட்டரி இணைக்க முடியாது.

நீங்கள் இன்னும் இணைத்தால், பெரிய சார்ஜ் கொண்ட பேட்டரி குறைந்த சார்ஜ் செய்யப்பட்ட பேட்டரியை சார்ஜ் செய்யும். இதன் விளைவாக, அவற்றின் மொத்த கட்டணம் குறைந்த மதிப்புக்கு குறையும்.

பொதுவாக, இந்த சேர்மங்களுக்கு இவை மிகவும் பொதுவான பயன்பாடுகளாகும்.

சிறந்த EMF ஆதாரம்

எலக்ட்ரோமோட்டிவ் ஃபோர்ஸ் (E) என்பது ஒரு இயற்பியல் அளவு ஆகும், இது சார்ஜ் கேரியர்களின் மூடிய சுற்றுகளில் இயக்கத்தின் மீது வெளிப்புற சக்திகளின் செல்வாக்கின் அளவை தீர்மானிக்கிறது. வேறு வார்த்தைகளில் கூறுவதானால், மின்னோட்டம் கடத்தி வழியாக எவ்வளவு வலுவாக பாய்கிறது என்பது EMF ஐப் பொறுத்தது.

இத்தகைய புரிந்துகொள்ள முடியாத நிகழ்வுகளை விளக்கும் போது, ​​உள்நாட்டு பள்ளி ஆசிரியர்கள் ஹைட்ராலிக் ஒப்புமைகளின் முறைக்கு திரும்ப விரும்புகிறார்கள். ஒரு கடத்தி ஒரு குழாய் என்றால், மின்சாரம் என்பது அதன் வழியாக பாயும் நீரின் அளவு, பின்னர் EMF என்பது திரவத்தை பம்ப் செய்ய ஒரு பம்ப் உருவாகும் அழுத்தம்.

எலக்ட்ரோமோட்டிவ் ஃபோர்ஸ் என்ற சொல் மின்னழுத்தம் போன்ற கருத்துடன் தொடர்புடையது. அவள், EMF, வோல்ட்களிலும் அளவிடப்படுகிறது (அலகு - "V"). பேட்டரி, ஜெனரேட்டர் அல்லது சோலார் பேனல் என ஒவ்வொரு சக்தி மூலமும் அதன் சொந்த மின்னோட்ட சக்தியைக் கொண்டுள்ளது. பெரும்பாலும் இந்த EMF வெளியீட்டு மின்னழுத்தத்திற்கு (U) அருகில் உள்ளது, ஆனால் எப்போதும் அதை விட சற்று குறைவாக உள்ளது. இது மூலத்தின் உள் எதிர்ப்பால் ஏற்படுகிறது, இதில் மின்னழுத்தத்தின் ஒரு பகுதி தவிர்க்க முடியாமல் குறைகிறது.

இந்த காரணத்திற்காக, EMF இன் சிறந்த ஆதாரம் ஒரு சுருக்கமான கருத்து அல்லது நிஜ உலகில் இடமில்லாத ஒரு இயற்பியல் மாதிரியாகும், ஏனெனில் பேட்டரி ரின் உள் எதிர்ப்பு மிகவும் குறைவாக இருந்தாலும், முழுமையான பூஜ்ஜியத்திலிருந்து வேறுபட்டது.

emf இன் சிறந்த மற்றும் உண்மையான ஆதாரம்

வேறுபட்ட வடிவத்தில்

சூத்திரம் பெரும்பாலும் வேறுபட்ட வடிவத்தில் வழங்கப்படுகிறது, ஏனெனில் கடத்தி பொதுவாக ஒத்திசைவற்றது மற்றும் அதை மிகச்சிறிய பகுதிகளாக உடைக்க வேண்டியது அவசியம். அதன் வழியாக செல்லும் மின்னோட்டம் அளவு மற்றும் திசையுடன் தொடர்புடையது, எனவே இது ஒரு அளவிடல் அளவு என்று கருதப்படுகிறது. ஒரு கம்பி வழியாக விளைந்த மின்னோட்டத்தைக் கண்டறியும் போதெல்லாம், அனைத்து தனி மின்னோட்டங்களின் இயற்கணிதத் தொகை எடுக்கப்படும். இந்த விதி அளவுகோல் அளவுகளுக்கு மட்டுமே பொருந்தும் என்பதால், மின்னோட்டம் ஒரு அளவிடல் அளவாக எடுத்துக்கொள்ளப்படுகிறது. தற்போதைய dI = jdS பிரிவின் வழியாக செல்கிறது என்று அறியப்படுகிறது. அதன் மின்னழுத்தம் Edl க்கு சமம், பின்னர் ஒரு நிலையான குறுக்குவெட்டு மற்றும் சம நீளம் கொண்ட கம்பிக்கு, விகிதம் உண்மையாக இருக்கும்:

மாறுபட்ட வடிவம்

எனவே, திசையன் வடிவத்தில் மின்னோட்டத்தின் வெளிப்பாடு: j = E.

முக்கியமான! உலோகக் கடத்திகளின் விஷயத்தில், கடத்துத்திறன் அதிகரிக்கும் வெப்பநிலையுடன் குறைகிறது, அதே நேரத்தில் குறைக்கடத்திகளுக்கு அது அதிகரிக்கிறது. ஓமோவின் சட்டம் கடுமையான விகிதாச்சாரத்தை நிரூபிக்கவில்லை

உலோகங்கள் மற்றும் உலோகக் கலவைகளின் ஒரு பெரிய குழுவின் எதிர்ப்பானது முழுமையான பூஜ்ஜியத்திற்கு நெருக்கமான வெப்பநிலையில் மறைந்துவிடும், மேலும் இந்த செயல்முறை சூப்பர் கண்டக்டிவிட்டி என்று அழைக்கப்படுகிறது.